(diese Seite wird noch bearbeitet - letztes Update: 29.06.2017)

Physik

...ist die wissenschaftliche Erforschung der Natur.

Mittlerweile sind unter diesem Begriff viele Bereiche vereint. Dazu gehören u.a.: Mechanik, Kinetik, Akustik, Optik, Elektrizitätslehre, Astronomie und sogar Atom- und Quantenphysik.

Diese Seite ist das Ergebnis einiger Jahre Nachhilfe für Abiturienten.
Sie beschreibt und erklärt (iagK) einige grundlegene Dinge der Physik. Aber zuerst ein paar "Basics"...

Maße und Einheiten

In der Physik sollte man immer mit den zugehörigen Einheiten rechnen. Nachfolgend sind einige gebräuchliche Maße und Einheiten aufgelistet (zuerst die sieben sog. Basiseinheiten).

Die sieben Basiseinheiten

	Formelzeichen	Einheit
Länge/Strecke	s	Meter: m
Masse	m	Gramm: g Tonne: t (1t = 1.000 kg)
Zeit	t	Sekunde: s Stunde: h (1h = 3.600 s)
Stromstärke magn. Durchflutung	I	Ampere: A = C / s = W / V
Temperatur	T t	Kelvin: K Grad Celsius: °C
Stoffmenge	n	Mol: mol
Lichtstärke	Iv	Candela: cd

Weitere Einheiten

	Formelzeichen	Einheit
Ebener Winkel	Radiant: rad	1
Raumwinkel	Steradiant: sr	1
Fläche	A	m2
Volumen	V	m3 Liter: l (1l = 1dm3)
Frequenz (Schwingungen/Sekunde)	f; v	Hertz: Hz = 1 / s

Die meisten Einheiten werden mit Zusätzen für Zehnerpotenzen versehen.

Formeln, Verhältnisse und abgeleitete Einheiten

	Formelzeichen	Einheit
Gewichtskraft	F = m · g	Newton: N = kg · m / s2
Druck	p = F / A	Pascal: Pa = N / m2 = kg / (m · s2)
Energie Arbeit Wärmemenge	E W Q	Joule: J = N · m = W · s = kg · m2 / s2
Leistung	P	Watt: W = J / s = V · A
elektrische Ladung	Q = I · t	Coulomb: C = A · s
elektrische Spannung	U = R · I	Volt: V = W / A = J / C = Ω · A
elektrische Kapazität	C = Q / U	Farad: F = A · s / V
elektrischer Widerstand	R = U / I	Ohm: Ω = V / A
elektrischer Leitwert	G = 1 / R = I / U	Siemens: S = 1 / Ω
magnetischer Fluss	Φ	Weber: Wb = V · s
magnetische Flussdichte Induktion	B	Tesla: T = Wb / m2
Induktivität	L; M	Henry: H = Wb / A
Lichtstrom	Φv	Lumen: lm = cd · sr
Beleuchtungsstärke	Ev	Lux: lx = lm / m2
Radioaktivität	A; a	Becquerel: Bq = 1 / s
Dichte (Massendichte)	Rho: ρ = m / V	kg / m3
Wichte (spez. Gewicht)	Gamma: γ = F / V	N / m3
Geschwindigkeit	v = s / t	m / s
Beschleunigung	a = s / t2	m / s2

Einige Naturkonstanten

Gravitationskonstante (für die Erde)	g = 9,81 m/s2
Lichtgeschwindigkeit (im Vakuum)	c = 299.792.458 m / s ~ 3 · 108 m / s

Generell sollte man in der Physik immer die korrekten Einheiten mitführen. Wer das nicht will, sollte sich mit Mathematik beschäftigen ;)

Nach oben

Nachfolgend werden einige häufig auftretende Themen erklärt und teilweise durch "typische" Beispielaufgaben ergänzt.

Mechanik

Statik (Lehre vom Gleichgewicht)

Die Statik ist ein Teilgebiet der Mechanik, das sich mit dem Gleichgewicht von Kräften an Körpern befasst. Die Gleichgewichtsbedingung der Statik besagt, dass ein ruhender (bzw. sich unbeschleunigt bewegender) Körper in Ruhe bleibt (bzw. sich unbeschleunigt bewegt), wenn die Summen aller Kräfte und Momente, die auf diesen Körper wirken, Null ist.

Nach oben

Kinematik (Bewegungslehre)

Die Kinematik ist die Lehre der Bewegung von Punkten und Körpern im Raum. Diese werden durch den Ort, die Geschwindigkeit (incl. Richtung) und der Beschleunigung (ebenfalls incl. Richtung) beschrieben.

Dabei gilt		bei const. Geschwindigkeit	bei const. Beschleunigung
Weg/Strecke	s [ m ]	s(t) = s0 + v · t	s(t) = s0 + v0 · t + 1/2 · a · t2
Geschwindigkeit	v [ m/s ]	const.	v(t) = v0 + a · t
Beschleunigung	a [ m/s2 ]	0	const.

Beispielaufgabe 1

Beispielaufgabe 2

Nach oben

Dynamik (Kinetik)

Die Dynamik ist die Lehre der Bewegung von Körpern unter Einfluss von Kräften.

Der Grundsatz der Dynamik lautet

Die Kraft F eines Gegenstandes, ist also das Produkt aus seiner Masse m [kg] und der Beschleunigung a [m/s²], die auf ihn wirkt.

Da jeder Gegenstand (auf der Erde) der Erdbeschleunigung von g = 9,81 m/s² *) unterliegt, ist die Gewichtskraft eines Gegenstandes also F = m · g.

Eine Masse von 1 kg hat also eine Gewichtskraft F = 1 kg · 9,81 m/s² = 9,81 N.

...

*) Die Erdbeschleunigung hängt vom genauen Ort (und dabei hauptsächlich vom Breitengrad) ab und liegt etwa bei 9,81 m/s². Allerdings rechnet man oft mit der Näherung von 10 m/s².

Nach oben

Schwingungen & Wellen

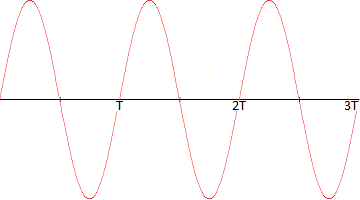
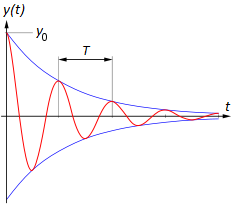Schwingungen & Wellen treten in vielen Varianten auf. Sie begegnen uns häufig bei Kreisfunktionen & Pendeln aber ebenso in der Akustik, der Optik & weiteren Bereichen.

Eine periodische (gedämpfte) Schwingung ist dabei ein Durchlauf einer sich (gedämpft) wiederholenden Funktionsfolge.

Eine harmonische Schwingung kann durch eine Sinusfunktion beschrieben werden.

Die Schwingungs- oder Periodendauer T [ s ] gibt die Dauer einer Schwingung an.
Der Kehrwert davon ist die Frequenz f = 1/T [ Hz = s^-1 = 1/s ].
Die Amplitude y oder y_max ist der maximale Ausschlag der Schwingung.
Der Ausschlag zum Zeitpunkt t wird mit y(t) angegeben.



...

Nach oben